Abstract
If you have ever tried to hit a target (such as a trash can) with a wad of paper, you know that aim is everything. But it is not always easy to get it right every time! Missing is not that big a deal with a wad of paper, but what if you were in an invading army in the Middle Ages, using a catapult to hurl huge stones and knock down castle walls? For a successful invasion, it would be important to know exactly how far, and how reliably, a catapult could launch a projectile. In this project you will use a toy catapult to launch ping pong balls and measure the distance they travel — and see if you can find the most reliable settings to hit a target from a certain distance.Summary
Ben Finio, Ph.D., Science Buddies
- Xpult is a registered trademark of Peloton Systems LLC.
- Wiffle is a registered trademark of The Wiffle Ball, Inc.
- Excel is a registered trademark of Microsoft Corporation.
Objective
Measure the distance balls travel when launched from a catapult, and use the results to construct a histogram and assess the catapult's reliability.
Introduction
Imagine that you were commanding an army in the Middle Ages and needed to use your catapult to hit a castle wall from a certain distance away — you would definitely need to know the most reliable way to launch the ball into the wall. Similarly, in this project you will use a toy catapult to launch a ping pong ball and measure the distance it travels. The catapult makes it easy to launch balls repeatedly with the same intended settings for the catapult (we will explain those settings later) — but, due to small, random changes in these settings, the ball will not travel exactly the same distance every single time. You will try to find different settings that can launch a ball the same distance, and then construct a histogram of your results to see which settings are more reliable.
A histogram is a graphical way to display how many things in a set of data fall into a certain numerical range (similar to a bar graph, but not quite the same). Figure 1 shows an example histogram and bar graph displaying weight and country of birth for 100 people. The histogram you make for this project will be similar to the one in Figure 1, except you will use the distance the ball travels instead of the weight of a person.
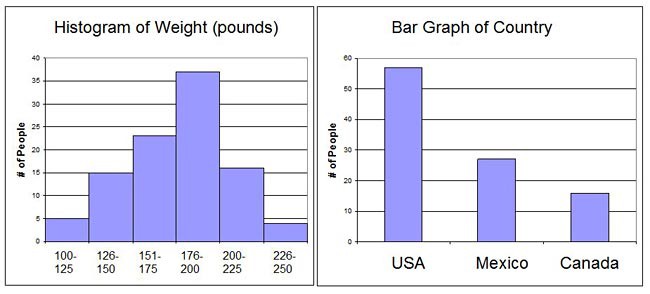 Image Credit: Ben Finio, Science Buddies / Science Buddies
Image Credit: Ben Finio, Science Buddies / Science BuddiesHistogram of weight in pounds (left) and a bar chart showing country of origin (right) for 100 people who reported their weight in pounds. The histogram has 6 ranges of weights that account for all weights between 100 and 250 pounds and resembles a normal distribution. The bar graph is arranged from largest to smallest populations: USA, Mexico and Canada.
Figure 1. An example of a histogram (left) and a bar graph (right) with data collected from 100 people who reported their weight and country of birth. The histogram shows how many people fall into a weight range — for example, 15 people weighed between 126 and 150 pounds. The bar graph shows how many people fall into a (non-numeric) category — for example, Mexico was named as home country by 27 people.
Constructing a histogram will also help you tell if your data follows a normal distribution. A normal distribution follows a "bell-shaped" curve, so you may frequently hear it referred to as a bell curve (less commonly it can also be referred to as a Gaussian distribution, named after the mathematician Carl Friedrich Gauss). The values of the mean and standard deviation, which you can calculate for your data, help describe the distribution.
Sometimes the words "mean" and "average" are used interchangeably, but technically that is not correct. "Average" can refer to one of three things — the mean, median, or mode. These are calculated three different ways:
- Mean: add up all the numbers and divide by how many numbers there are.
- Median: list the numbers in order from smallest to largest and take the middle number.
- Mode: take the number that occurs most often.
For example, say we have five numbers: 9, 5, 8, 9, and 3.
- The mean is (9+5+8+9+3)/5 = 6.8
- The median when the numbers are listed in order from lowest to highest (3,5,8,9,9) is 8.
- The mode is 9, because it occurs the most (twice, while all the other numbers appear only once).
So the mean, median, and mode are all different in this case — but any one of them can be called an "average" for this set of numbers.
The mean is the location of the middle of the curve, and the standard deviation measures how "spread out" the curve is. When referring to an entire population (every possible measurement you can make), the mean and standard deviation are represented by the Greek letters μ and σ, respectively. When working with a sample (a subset of the population), the mean is represented by x̄ and the standard deviation by s. For example, if your variable is "height of a person," the population would be every person on the planet — around 7 billion people! — so it is much more realistic to take a smaller sample of that population.
Figure 2 shows two examples of normal distributions with different means and standard deviations.
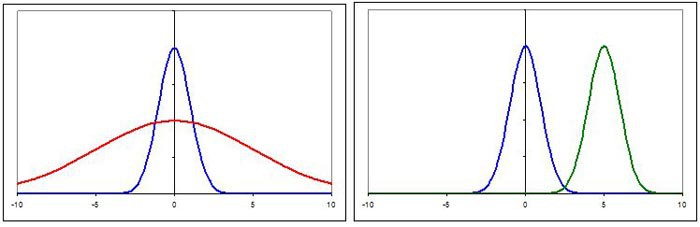 Image Credit: Ben Finio, Science Buddies / Science Buddies
Image Credit: Ben Finio, Science Buddies / Science Buddies
Figure 2. Examples of normal distributions. On the left, the two curves have the same mean (zero), but the red curve is more spread out — it has a larger standard deviation. On the right, the two curves have the same shape (and thus the same standard deviation), but different means (0 for the blue curve and 5 for the green curve).
If your histogram "fits" nicely under a bell curve, then your data is probably normally distributed (this is a simplification that may make some mathematicians unhappy, but it is OK for the purposes of this project; for a more advanced explanation of normal distributions, see the Bibliography). Figure 3 shows examples of two different histograms — one that appears to fit a normal distribution, and one that does not.
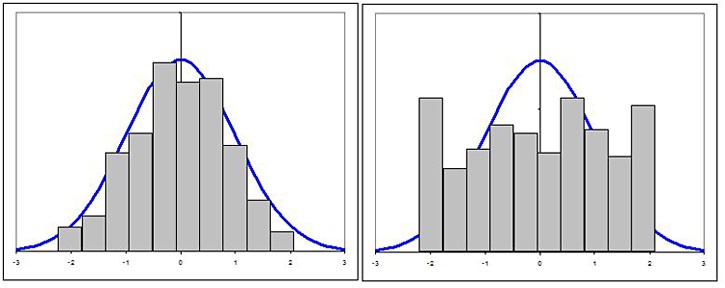 Image Credit: Ben Finio, Science Buddies / Science Buddies
Image Credit: Ben Finio, Science Buddies / Science Buddies
Figure 3. Examples of two histograms compared to the same bell curve. The histogram on the left appears to follow the general shape of a bell curve (though not perfectly). The histogram on the right does not, so the data is probably not normally distributed.
The assembled catapult kit is pictured in Figure 4, with all of its parts labeled. The catapult has two key features: an adjustable pin lets you set the launch angle (the angle the ball travels relative to the ground, or "horizontal," at launch) and tick marks let you measure the pull-back angle (how far back the arm is pulled before launch). Figure 5 shows a zoomed-in view of how to measure these angles and Figure 6 labels them for clarity. The catapult kit also comes with two different balls (ping-pong and Wiffle®) and enables you to adjust the number of rubber bands (one, two, or three). The Bibliography contains more information about the catapult kit; the important thing for this project is that you know there are four variables you can adjust, and each of these will affect how far the ball goes:
- Launch angle
- Pull-back angle
- Type of ball
- Number of rubber bands

A catapult kit is made up of 3 main parts which include the base, disc and arm. The base is secured to a flat surface using an included clamp. The base and arm are both connected to a rotating disc that allows the arm to swing back and forth freely. A locking pin is inserted into the base and disc so only the arm may move freely. A rubber band connects the base of the arm to the disc so when the arm is pulled back the rubber band will launch it forward. At the end of the arm a small cup holds a ping pong ball that will be launched when the catapult is completely assembled.
Figure 4. An assembled catapult with all of its parts labeled. The rubber-band powered catapult is clamped to a table (with a paper towel between the clamp and the table to prevent it from scratching the surface). An aluminum disk with tick marks lets you easily measure the launch angle and pull-back angle.
 Image Credit: Ben Finio, Science Buddies / Science Buddies
Image Credit: Ben Finio, Science Buddies / Science Buddies
Figure 5. Tick marks enable you to read the launch angle and the pull-back angle on the catapult disk. In this picture the launch angle is 30 degrees and the pull-back angle is 60 degrees.
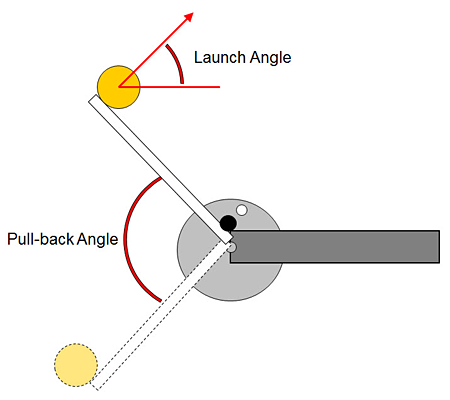 Image Credit: Ben Finio, Science Buddies / Science Buddies
Image Credit: Ben Finio, Science Buddies / Science Buddies
Figure 6. Illustration of the launch angle and pull-back angle.
In this project, you will choose parameters for each of these four variables (launch angle, pull-back angle, type of ball, and number of rubber bands), and measure how far the ball travels when launched over many trials. You will calculate the mean and standard deviation of your data and construct a histogram, and then use this information to see if you can find some settings that produce more reliable results than others.
Terms and Concepts
Make sure you understand the following terms before you continue with the project.
- Histogram
- Bar graph
- Normal distribution
- Bell curve
- Gaussian distribution
- Standard deviation
- Average
- Mean
- Median
- Mode
- Population
- Sample
- Launch angle
- Pull-back angle
- Bin size
Questions
- How repeatable do you think shots from the catapult will be? Do you think you will be able to consistently hit a target within one inch? Two inches? A foot?
- How do you think the mean and standard deviation of your data will change if you change the launch settings of the catapult? Will some settings be more reliable than others?
- Do you think the data you collect will be normally distributed? Why or why not?
Bibliography
The following references can help you learn more about normal distributions and histograms. The Math Is Fun website is the easiest to read for beginners; the Wikipedia and Wolfram Mathworld pages are more advanced.
- MathIsFun.com. (n.d.). Normal distribution. Retrieved October 18, 2012.
- MathIsFun.com. (n.d.). Histograms. Retrieved October 18, 2012.
- MathIsFun.com. (n.d.). Standard deviation formulas. Retrieved October 18, 2012.
- Wikipedia contributors. (2012, October 14). Normal distribution. Wikipedia, the Free Encyclopedia. Retrieved October 18, 2012.
- Wikipedia contributors. (2012, October 4). Histogram. Wikipedia, the Free Encyclopedia. Retrieved October 18, 2012.
- Weisstein, E. W. (n.d.). Normal distribution. WolframMathWorld.com. Retrieved October 18, 2012.
Materials and Equipment 
Recommended Project Supplies
- Ping Pong Catapult Kit, available from our partner
Home Science Tools.
In addition to the catapult, will need these items from the kit:
- Three rubber bands, 3 × 1/8 inches
- Table tennis (ping pong) ball
- Plastic ball with holes (like a Wiffle® ball)
- Clamp for attaching the catapult to a surface
- You will also need to gather these items, not included in the kit:
- Surface for mounting catapult (piece of wood on the floor, tabletop, etc.)
- Optional: paper towels, dish towel, or other padding to keep the mounting surface from being scratched by the attachment clamp
- Open area for launching balls
- A second person (the data collection part of the project requires two people total - one person to operate the catapult, and one person to mark and record the distance the ball travels)
- Tape measure (12 ft. minimum)
- Lab notebook
Disclaimer: Science Buddies participates in affiliate programs with Home Science Tools, Amazon.com, Carolina Biological, and Jameco Electronics. Proceeds from the affiliate programs help support Science Buddies, a 501(c)(3) public charity, and keep our resources free for everyone. Our top priority is student learning. If you have any comments (positive or negative) related to purchases you've made for science projects from recommendations on our site, please let us know. Write to us at scibuddy@sciencebuddies.org.
Experimental Procedure
- Set up the catapult.
- Use the clamp to attach the catapult to the edge of a sturdy surface, like a table. Make sure you have plenty of open space (at least 12 feet [ft.]) in front of the catapult to launch the ball.
- Lay your tape measure out on the floor in front of the catapult (in the same direction you will be launching the ball), with the end reading "zero" inches lined up with the center of the catapult's disk. Once you have placed the tape measure on the floor, you may want to tape it to the floor. You do not want it to move during your experiments; otherwise, measurements will not be consistent.
- Select launch parameters for the catapult. Pick a launch angle, pull-back angle, type of ball, and number of rubber bands. Almost any settings you choose should work, but make sure they are sufficient to launch the ball a distance of at least a couple of feet. For example, a small pull-back angle of only 5 or 10 degrees, with just one rubber band, probably will not launch the ball very far, and this will make it difficult to take measurements (for example, if the ball doesn't even clear the base of the catapult).
- Launch the ball. One person should be operating the catapult and ensuring that all the settings selected in Step 2 are correct. The second person should be sitting or kneeling along the side of the tape measure (how far away from the catapult will depend on the settings you've selected). This person should pay very close attention to where the ball first hits the ground. Immediately mark this location with your finger (rather than just trying to remember it) — you do not want to record where the ball comes to a final stop after rolling or bouncing. Be sure to write this distance down.
- Now you are ready to start the data-collecting part of the project. Launch the ball at least 50 more times, with exactly the same settings you used in step 2.
- The most difficult setting to repeat is the pull-back angle, because it is set by hand and can be adjusted continuously (as opposed to the launch angle, which is set by the pin shown in Figure 4 and can be adjusted in 15 degree increments only). So, whoever is operating the catapult must be careful to use exactly the same pull-back angle each time.
- Remember to record where the ball first hits the ground and not how far it bounces or rolls. You can round to the nearest inch when measuring, as it will be difficult to accurately measure to within fractions of an inch. It may help to record your results with tick marks in a table (this will make it easier to make a histogram later). See Table 1 for an example.
- If you have the time and patience, you can certainly do more than 50 trials. The more data you have, the better your histograms will be.
| Distance (in inches) |
Number of Trials |
|---|---|
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 |
- Calculate the mean and standard deviation of your data. You can do this by hand or
with a spreadsheet program such as Microsoft Excel®.
- To calculate the mean x̄ by hand, add up all the values and then
divide by the total number of trials. For example (using five trials to keep
the example short), say your measured distances were 52, 54, 57, 57, and 61
inches. The mean is the sum of all the distances divided by the number of
trials: the numbers add up to 281, and there are five trials — so,
dividing 281 by 5 gives the mean of 56.2:
Equation 1:
(Note: Hover over the equations in this Procedure with your cursor to view enlarged formulas.)In general, the equation to calculate the mean is
Equation 2:
- N is the total number of trials
- i is the index used to keep track of each trial, starting at 1 and going up to N
- xi is the value for a trial at index i
- x̄ is the mean
- (Skip this step if you are not using Excel®). To calculate the mean in Excel®, enter all of the values (52, 54, 57, 57, 61) in a single column or row, and then use the AVERAGE() command. For example, if you typed your values into column A in rows 1 through 5, you would type =AVERAGE(A1:A5) into any other cell to calculate the mean.
Technical Note:
We stated in the Introduction that "mean" and "average" are sometimes used interchangeably, even though this is not technically correct. Here is a perfect example — Excel® uses the command AVERAGE() to calculate the mean. It has separate commands for MEDIAN() and MODE().
- The formula to calculate standard deviation by hand is a bit more complicated. It might look scary at first, but do not worry. It is actually not that hard to calculate. The formula for standard deviation is:
Equation 3:
- N is the total number of trials
- i is the index used to keep track of each trial, starting at 1 and going up to N
- xi is the value for a trial at index i
- x̄ is the mean
- s is the standard deviation
We will break this down into steps using our example data to make it easier to understand. The first thing to do is take the difference between each of the individual values and the mean you calculated — that is, the (xi - x̄) part of the equation. So, for our data, (52, 54, 57, 57, 61), and our mean, 56.2, that comes out to:
- 52 - 56.2 = -4.2
- 54 - 56.2 = -2.2
- 57 - 56.2 = 0.8
- 57 - 56.2 = 0.8
- 61 - 56.2 = 4.8
Next you have to square each one of those numbers — notice how the (xi - x̄ ) part of the equation is squared. So, we have:
- -4.22 = 17.64
- -2.22 = 4.84
- 0.82 = 0.64
- 0.82 = 0.64
- 4.82 = 23.04
Now we have to add all of those numbers up — that is what the symbol means. Now we get:
- 17.64 + 4.84 + 0.64 + 0.64 + 23.04 = 46.8
Almost done! Notice the 1/(N-1) inside the square root. So now we have to divide this number by N-1 (in this case N = 5):
- 46.8/(5-1) = 11.7
And finally, we take the square root of that number to solve for s:
- (Skip this step if you are not using Excel®). You can also calculate the standard deviation in Excel® using the STDEV() function. This will be easier than doing it by hand for a very large amount of data. For example, if you enter your five values into cells A1 through A5, you would type =STDEV(A1:A5) in another cell to calculate the standard deviation.
Technical Note:
There is a slight difference in the calculation for standard deviation if you are using an entire population instead of just a sample. Here we are assuming that your data is just a sample of all possible shots that can be taken with the catapult, because you can always do more trials. For an entire population, the equation is
The only practical difference, aside from changing the letters used for the variables, is that the (N-1) in the denominator changed to just an N. We will not go into the details for this here, but if you are curious, search for "Bessel's Correction" online.
- To calculate the mean x̄ by hand, add up all the values and then
divide by the total number of trials. For example (using five trials to keep
the example short), say your measured distances were 52, 54, 57, 57, and 61
inches. The mean is the sum of all the distances divided by the number of
trials: the numbers add up to 281, and there are five trials — so,
dividing 281 by 5 gives the mean of 56.2:
- By now you should have run through at least 50 trials for one set of catapult settings (launch angle, pull-back angle, ball type, and number of rubber bands), recorded the distance for each launch, and calculated the mean and standard deviation. For your next step, find new catapult settings that launch the ball about the same distance. For example:
- Say you were using two rubber bands to launch the ball about 70 inches. Can you do this with just one rubber band by changing the other parameters?
- If you were hitting a certain distance with a 30-degree launch angle, can you also hit that distance with a 75-degree launch angle? How?
- Finding the new settings will take a bit of trial and error.
- Repeat steps 3 through 5 for these new launch settings.
- Compare the mean and standard deviation for each of your experiments. Does one set of data have a smaller standard deviation? If so, this indicates that those settings were more reliable. Why do you think that happened?
- Construct histograms for both of your data sets. Remember that the standard deviation will correspond to how "spread out" the histogram looks. You may also need to adjust the bin size of your histogram. For example, say that for more than 50 shots, your shortest distance was 58 inches and your longest was 72 inches. Your histogram might not look right if you have a bar for every one-inch increment — it may be better to have larger "bins", such as 58 to 61 inches, 61 to 64 inches, 64 to 67 inches, and so forth. If you need more help understanding this concept, refer to the FAQ on histograms below.
- Does your data look normally distributed? Are your histograms symmetric, or skewed to one side? Can you explain why they look the way they do?
Troubleshooting
For troubleshooting tips, please read our FAQ: Bet You Can't Hit Me! The Science of Catapult Statistics.
Ask an Expert
Global Connections
The United Nations Sustainable Development Goals (UNSDGs) are a blueprint to achieve a better and more sustainable future for all.
Variations
- If you have time, continue to find as many different combinations of settings as you can to launch the ball the same distance. Calculate the mean and standard deviation for each. What are the most reliable settings you can find?
- What happens if you change the relative elevations of the catapult and landing area (for example, clamping the catapult to a table and launching the ball onto the floor, or the other way around)? Does this change the shape of your histograms?
Frequently Asked Questions (FAQ)
The Science Buddies catapult kit is used in four projects:
- Bombs Away! A Ping Pong Catapult
- Under Siege! Use a Catapult to Storm Castle Walls
- Launch Time: The Physics of Catapult Projectile Motion
- Bet You Can't Hit Me! The Science of Catapult Statistics
The FAQs below are used for all four projects. General catapult questions are at the top of the FAQs list and project specific questions are at the bottom of the list.
 Image Credit: Ben Finio, Science Buddies / Science Buddies Image Credit: Ben Finio, Science Buddies / Science Buddies
|
 Image Credit: Ben Finio, Science Buddies / Science Buddies Image Credit: Ben Finio, Science Buddies / Science Buddies
|
 Image Credit: Ben Finio, Science Buddies / Science Buddies Image Credit: Ben Finio, Science Buddies / Science Buddies
|
Note: On older versions of the Xpult brand catapult, the pull-back angle may be read from the bottom edge of the launch arm. If you just ordered a new Science Buddies catapult kit for your project (as of October 2012), then you should follow the directions above.
Depending on your camera, you may also be able to manually adjust settings and decrease the exposure time. Consult your camera's manual to see if that is possible.
If your theoretical and experimental results are very different, there are a couple things you can check:
- Are your theoretical predictions reasonable? You should be able to launch the ball across an average-sized room in your house — meaning it should go a couple meters before it hits the ground, for typical catapult settings. If your predictions indicate that the ball will travel several kilometers, or only a couple millimeters, then odds are you made a mathematical mistake. Double-check your calculations, and be extra careful to look for typos if you entered equations into a spreadsheet program.
- Make sure you properly used a scale factor to convert the distances you measure on your computer screen to real-world distances for your experimental data. Again, make sure the distance the ball travels is reasonable — if your experimental data says that the ball traveled 100 meters, then you probably used the scale factor incorrectly.
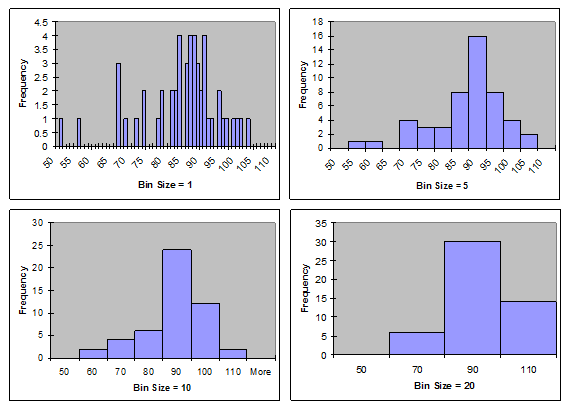 Image Credit: Science Buddies
Image Credit: Science BuddiesFour example histograms display the same data with bin sizes of 1, 5, 10 and 20. As the bin sizes change, the distribution of data becomes too compact or spread out to determine whether or not the data is normally distributed from a glance. Bin sizes of 5 and 10 show a clearly normal distribution of data, but bin sizes of 1 and 20 are less obvious.
Notice how the shape of the distribution is evident with bin sizes of 5 or 10, but rather difficult to see with bin sizes of 1 or 20. As a general rule of thumb, more data will allow you to use a smaller bin size, which will give you a more accurate picture of the distribution — so if you have time, try to do more than 50 trials with the catapult.
For the person recording distances, we recommend watching where the ball lands and immediately marking the location with your finger. Then take a reading from the tape measure. Trying to watch where the ball lands and simultaneously read the tape measure will be very difficult.
Also, you probably won't be able to get fraction-of-an-inch accuracy on your readings — getting the closest one-inch increment will be good enough.
Careers
If you like this project, you might enjoy exploring these related careers:
Contact Us
If you have purchased a kit for this project from Science Buddies, we are pleased to answer any question not addressed by the FAQ above.In your email, please follow these instructions:
- What is your Science Buddies kit order number?
- Please describe how you need help as thoroughly as possible:
Examples
Good Question I'm trying to do Experimental Procedure step #5, "Scrape the insulation from the wire. . ." How do I know when I've scraped enough?
Good Question I'm at Experimental Procedure step #7, "Move the magnet back and forth . . ." and the LED is not lighting up.
Bad Question I don't understand the instructions. Help!
Good Question I am purchasing my materials. Can I substitute a 1N34 diode for the 1N25 diode called for in the material list?
Bad Question Can I use a different part?
Contact Us











