Others Like “Exploring Fractals” (top 20 results)
|
A fractal is, "a rough or fragmented geometric shape that can be subdivided in parts, each of which is (at least approximately) a reduced/size copy of the whole" (Mandelbrot, 1982). There are many different fractal patterns, each with unique properties and typically named after the mathematician who discovered it. A fractal increases in complexity as it is generated through repeated sets of numbers called iterations. There are many interesting projects exploring fractal geometry that go beyond…
Read more
This is a great project for someone interested in both stargazing and photography. Bright city lights and even the light of the full Moon obscure the dimmest stars, which can make identifying constellations more difficult. In this astronomy science project, you will calibrate a digital camera to measure the skyglow in different locations. This can be a great tool to comparing the quality of different star viewing locations.
Read more
You've probably noticed the colorful patterns "reflecting" from the shiny surface of a CD disk. What you are seeing is actually diffraction of white light, and the rainbows of color are diffraction patterns. In this project you'll learn about how diffraction patterns are generated, and you'll find out how you can use a laser pointer and a protractor to measure the microscopic spacing of data tracks on a CD.
Read more
Digital cameras can be a great way to learn about photography. Most digital cameras today have LCD screens, so you get instant feedback on your photo. If you make a mistake, no problem, you just delete the picture. It's nice that you don't have to worry about the expense and bother of developing film! This project can help you learn to take better pictures.
Read more
Do you have a favorite picture? When you have a photo that you treasure, you want it to look as good as possible. Find out how the resolution of a digital photo effects the way it looks when you print it out. How does the quality of the image relate to the resolution?
Read more
How many bits of information are in a digital photo? It depends on how many possible colors there are. Learn how to choose the right number of colors and bits to post your photo on the web or send it to your best friend.
Read more
What do you do if you take a photo and it turns out too dark or too bright? You can use your computer to fix it for you.
Read more
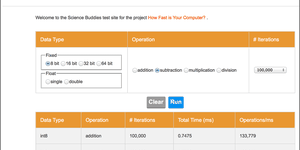
How fast are computers? How quickly do you think they can do 100 million arithmetic problems? Try this science project to discover an easy way to measure how fast computers have become and whether or not your computer is a math whiz.
Important: this project was originally written in the mid-2000's, and computers have gotten a lot faster since then! The project will probably not work as intended if you run the code on a modern computer.
Read more
Have you ever wanted to analyze data from a NASA spacecraft? In this science project you will use data from NASA's MESSENGER mission to measure the diameter and calculate the depth of impact craters on Mercury. You will then analyze that data for relationships between a crater's depth and diameter. This is your chance to
perform a science project as a NASA researcher would!
Read more
This is a modern version of a classic experiment by Robert Boyle on the compressibility of gases. Boyle discovered the relationship between pressure and volume of gases that now bears his name. This project shows you a simple method for re-creating this famous experiment.
Read more
|
Explore Our Science Videos
Make Candy Gears - STEM activity
Build A Solar Updraft Tower!
Storm Surge Activity - Protect Houses From Waves