Abstract
Want to stretch your imagination? One good way is to try to imagine how far it is to a distant star. How much farther away is it than the moon is from the earth? How much farther away than the earth is from the sun? How long would it take to get there? In this project, you'll learn one way of measuring the distance without leaving Earth.Summary
Andrew Olson, Ph.D., Science Buddies
Sources
This project is based on:
- Blanchard, P.K., 2004. Stellar Parallax. California State Science Fair Abstract. Retrieved December 4, 2006.

Objective
The goal of this project is to measure the distance to some distant, small objects using motion parallax.
Introduction
Try this: hold a pencil straight in front of you at arm's length. Close one eye and line the pencil up with a distant object (e.g., a light switch on the wall across the room). Now, without moving the pencil, close the other eye and look at the pencil. The pencil appears to move—it is no longer aligned with the distant object. What happened?
Because of the distance between your two eyes, each eye views the pencil from a slightly different angle (labeled P in Figure 1). By alternately viewing the pencil with each eye alone, you are changing your point of view by the distance that separates your eyes. Each eye alone will see the pencil aligned at a different position on a distant background. Thus, when you close one eye and then the other, the pencil appears to move relative to the background.
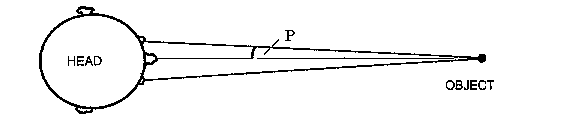 Image Credit: Margaret Penston
Image Credit: Margaret Penston
Figure 1. If you view an object held at arm's length first through one eye and then through the other, the object appears to move relative to a more distant background. This is an example of motion parallax.
What you are seeing with the pencil is an example of motion parallax, the apparent motion of an object against a distant background due to motion of the observer. Astronomers can use motion parallax to measure the distance to stars that are relatively close to earth. With the distances involved, the trick of simply closing one eye and then the other doesn't work for stars. You need a much bigger distance between the two observations than the distance between your eyes. Astronomers take advantage of the earth's travel in its orbit around the sun to obtain the maximum separation between two observations of a star (see Figure 2). The parallax angle, P, is measured by comparing the nearby star's position to the stable position of distant background stars.
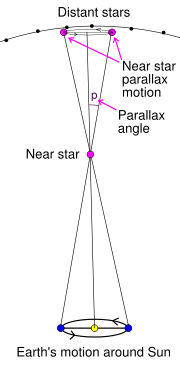
Figure 2. Astronomers can use motion parallax to measure the distance to nearby stars. They take advantage of the earth's travel in its orbit around the sun to obtain the maximum distance between two measurements. The star is observed twice, from the same point on earth and at the same time of day, but six months apart. (Wikipedia, 2006b
Terry Herter, a professor of astronomy at Cornell University, has written a cool interactive Java applet that illustrates how astronomers use motion parallax to measure distances to nearby stars (Herter, 2006). You can click and drag on the star in the applet to change its distance from earth. When you do, you will see how its apparent motion for an observer on earth changes with its distance from earth.
How is the distance from earth to the star calculated? The method is called triangulation, because you are using the properties of triangles to measure the distance. In this case it is a right triangle, with the sun forming the vertex of the right angle. The length of the short side of the triangle (distance from the earth to the sun) is known. The parallax angle is measured from observations of the nearby stars motion relative to distant background stars. Astronomers can make this measurement using photographs taken with the telescope. They can measure the angle of the nearby star's motion because they have previously calibrated the angle subtended by the field of view of the telescope.
The motion is measured in angular units called arc seconds. (One degree of arc can be divided into 60 arc minutes, and each minute of arc can be divided into 60 arc seconds. So an arc second is 1/3600th of a degree.) The parallax angle, p is equal to one half of the observed motion, measured in arc seconds (see Figure 2).
Here is the equation used for calculating the distance to a nearby star (you can read how this equation was derived in the Wikipedia article on parallax (Wikipedia contributors, 2006a)):
The distance from the Earth to a star is equal to the distance from the Earth to the Sun multiplied by 180, multiplied by 3600 and then divided by the product of the parallax angle and pi.
The parallax angle, p, is given in arc seconds.
You can use a similar technique to measure the distance of objects that you observe with a telescope. For astronomers, the background objects against which nearby stars are measured is essentially at infinity. The angular motion is measured by calibrating the angle of view of the telescope, and making measurements from photographs. You'll make your measurements with a known distance from the object to a calibration grid behind the object. You'll use the parallax angle and similar triangles to figure out the distance between the object and the telescope. The Experimental Procedure section shows how you can do this on a football field.
Terms and Concepts
To do this project, you should do research that enables you to understand the following terms and concepts:
- Motion parallax
- Similar triangles
- Arc minutes
- Arc seconds
Bibliography
- This webpage has an interactive animation that shows how astronomers use stellar parallax to measure how far a star is from Earth. You can click and drag to change the distance of the star from Earth, and see how the star's movement changes compared to distant background objects.
Purcell, C.R., (n.d.). Astronomical Parallax Simulation. Retrieved March 25, 2024. - Wikipedia has an excellent article on motion parallax. Pay special attention to the section on Parallax and measurement instruments. You'll need to know this material when carrying out your measurements for this project!
Wikipedia contributors, 2006a. "Parallax," Wikipedia, The Free Encyclopedia. Retrieved December 5, 2006. - Wikipedia also has a good explanation of arc minutes:
Wikipedia contributors, 2006b. Minute of Arc, Wikipedia, The Free Encyclopedia. Retrieved December 5, 2006.
Materials and Equipment
To do this experiment you will need the following materials and equipment:
- Telescope
- Long tape measure
- Easel
- Background grid with regular spacing (e.g., graph paper)
- Penny, washer, pencil, or similar small object
- Support from which to hang the small object (tripod, music stand, etc.)
- String
- Pencil
- Lab notebook
- Empty football field
Experimental Procedure
-
At one end of the field, set up the easel with the grid attached to it so that it is perpendicular to the ground. Position the grid at a convenient height for viewing straight-on with the telescope. Hang two small objects directly in front of the center of the grid at two different distances (d') from the easel. Measure and record the distance, d', for each object.
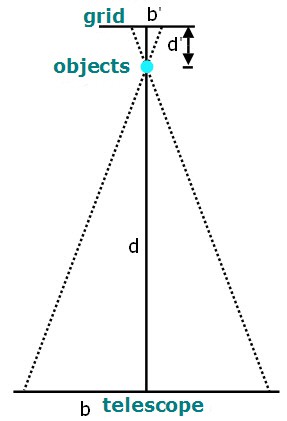
Figure 3. Diagram showing the similar triangles used to calculate the distance, d, from the telescope to the object. Note that the distance, d', from the object to the grid has been exaggerated to make the labeling clear.
- Set up your telescope approximately 100 meters away from the easel, so that it is directly in front of the grid. The objects should line up with the center of the grid when centered in the telescope. Mark the center line of the grid, and mark the position of the telescope.
- Now move the telescope one meter to the left, keeping it at the same height. Center the first object in the telescope, and use the grid to measure how far the object is from the center line (this is your b' measurement for the first object). Then center the second object in the telescope, and use the grid to measure how far the object is from the center line (this is your b' measurement for the second object).
- Now move the telescope one meter to the right of the straight-on position. Again, center each object and measure how far it is from the center line.
- Average your left and right measurements for each object to get b'.
- Use the ratio s'/b' = s/b to calculate the distance s from the telescope to each object.
- Is the distance between the two objects the same as what you get from your direct measurements?
- Use a tape measure to measure the distance from the telescope (center position) to the objects. How does the direct measurement compare to your parallax calculations?
Ask an Expert
Global Connections
The United Nations Sustainable Development Goals (UNSDGs) are a blueprint to achieve a better and more sustainable future for all.
Variations
- What is the smallest angle you can reliably resolve at 100 meters with a 2-meter baseline? Explain how this relates to the maximum distance you can measure with this set-up.
Careers
If you like this project, you might enjoy exploring these related careers:









