Abstract
In this project, you will make 2-dimensional templates, called nets, that fold up into 3-dimensional (3-D) shapes. By making shapes of different sizes, you will be able to see how 3-D shapes change with size. Which property (or aspect) will change the most: the length of an edge, the surface area, or the volume?Summary

Watch CYBERCHASE on PBS KIDS GO! Check local listings or visit CYBERCHASE. CYBERCHASE is produced by THIRTEEN in association with WNET. All rights reserved. CYBERCHASE is a trademark of THIRTEEN. The PBS KIDS GO! logo is a registered mark of PBS and is used with permission.
The sources for this project are the following games, activities, and episodes from CYBERCHASE on PBS KIDS GO!:
- Thirteen/WNET New York. (2008). (a). CYBERCHASE: 2D to 3D Morphing Game. Educational Broadcasting Corporation, New York. Retrieved October 24, 2011.
- Thirteen/WNET New York. (2008). (c). CYBERCHASE: Episode 113: Eureeka! Educational Broadcasting Corporation, New York. Retrieved December 6, 2007.
Sara Agee, PhD, Science Buddies

Objective
In this project, you will investigate how a 3-D object changes as it increases in size by measuring and comparing the length of an edge, the surface area, and the volume.
Introduction
Join the CyberSquad to investigate the shapes around us by watching CYBERCHASE on PBS KIDS GO! and by doing this fun experiment for your science fair.
Meet Harry from the CyberSquad as he tries to make a tall, 3-dimensional house out of flat, 2-dimensional pieces. Will he be able to build it? Check out the "For Real" video below and find out. Then read on to see how you can make 3-dimensional objects, like pyramids and cubes, with the help of some CyberSquad "morphing" tools.
Now you know that the world is full of shapes, but all shapes aren't flat! All of the objects we have and use are made of shapes. You can see in Figure 1 below how objects can be put into groups, based upon the shapes they have in common.
Flat shapes are called 2-dimensional (2-D) and they can be put together to fold up and form shapes that are 3-dimensional (3-D), which have depth to them. For example, a box that you put something in is a 3-D shape, but a drawing you make on a flat piece of paper is a 2-D shape. 2-D and 3-D shapes are often used in science and engineering for making models. Electrical diagrams and circuits are examples of 2-D models used in electrical engineering, and are important for building new technology. 3-D models of complex protein molecules are often used in chemistry and biology to unravel the secrets of disease.

Figure 1. Shapes image © 2007 TTS Group Ltd.
What are some common terms for 3-D shapes? Here is a collection of 3-D shapes in Figure 2. Notice that 3-D shapes have faces (sides), edges, and vertices (corners). The exception is a sphere (ball) which has no edges or vertices. (BBC, 2007):
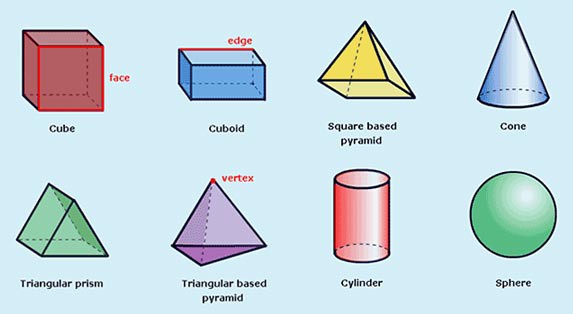
Figure 2. 3-dimensional (3-D) shapes have faces, edges, and vertices. (BBC, 2007; image ©2007 BBC.)
We live in a world of shapes, all with unique and interesting properties. Properties are certain qualities of an object that can be used to characterize that object. Geometry is the study of the properties of shapes in mathematics. Here are some properties of shapes that you may already have some experience with:
- Dimension - Dimension is a property of a shape, and tells us if the shape has depth. A school playground is 3-D, but a drawing you make on a flat piece of paper is 2-D.
- Length - The edges of a shape have a certain length. The length of the edges of a shape is what gives it a certain size, and can be measured. The faces of both 2-D and 3-D shapes have edges of certain length. You experience this property when you measure the edge of something with a ruler.
- Area - The amount of space the surface of one face takes up is called the area. If you put a shape on a piece of graph paper, the number of squares the face covers is the area. The area of a shape can be measured in square centimeters (cm2) and is a property of both 2-D and 3-D shapes. You have experience with this property when you notice that your friend got a bigger slice of pizza than you did.
- Surface Area - If you add together all of the areas from the faces of a 3-D shape, then the total is the surface area. It is the total amount of space needed to cover the outer surface of the shape. This is a property of 3-D shapes, and you might have noticed it when you've tried to figure out how much wrapping paper to use to wrap a present.
- Volume - The amount of space that a 3-D shape takes up is called volume. Volume can either be filled with a solid (like the chocolate in a chocolate bar), a liquid (like the amount of milk in a glass), or a gas (like the amount of air in an empty box). Volume is a property of 3-D, but not 2-D, objects and can be measured in cubic centimeters (cm3) or in milliliters (mL). In fact, one cubic centimeter of water is also 1 milliliter of water! You experience volume when you help make cookies and measure out the ingredients with measuring cups.
In this project, you will join the characters of the Cyberchase CyberSquad to make 2-D templates, called nets, that fold up into 3-D shapes. You will print and assemble the nets in one of the following shapes: a pyramid, a cube, or an octahedron. By printing the templates at different scales (50%, 75%, and 100%), you will be able to see how different properties of 3-D shapes change with size. Which property of a 3-D object will change the most as it increases in size: the length of an edge, the surface area, or the volume?
Terms and Concepts
To do this type of experiment you should know what the following terms mean. Have an adult help you search the Internet or take you to your local library to find out more!
- 2-dimensional (2-D)
- 3-dimensional (3-D)
- Faces
- Edges
- Vertices
- Sphere
- Property
- Dimension
- Length
- Area
- Surface area
- Volume
- Scale
- Morphing
Questions
- Which property of a 3-D object will change the most as it increases in size: the length of a side, the surface area, or the volume?
- How do you measure the length of an edge?
- How can you measure the surface area of a 3-D shape?
- How can you measure the volume of a 3-D shape?
Bibliography
Watch Cyberchase on PBS KIDS GO! Check local listings or visit www.pbskidsgo.org/cyberchase. This project is based on the following games, activities, and episodes from CYBERCHASE on PBS KIDS GO!:
- PBS Kids Go! Cyberchase. (2008). Activities: 2D to 3D Morphing Game. Thirteen/WNET. Retrieved January 11, 2022.
- PBS Kids Go! Cyberchase. (2008). Cyberchase: Episode 113: Eureeka! Thirteen/WNET. Retrieved January 11, 2022.
At BBC you can learn about the different 3-dimensional shapes:
- BBC. (2007). KS2 Bitesize Revisions: 3D Shapes. BBC, UK. Retrieved December 6, 2007.
At this site, you can download and print free centimeter graph paper:
- FEN. (2007). Centimeter Graph Paper. TeacherVision, Family Education Network (FEN) and Pearson Education, Inc. Retrieved December 6, 2007.
This site has a java applet you can use to make printable, color graphs of your data:
- NCES. (2006). Create a Graph. National Center for Education Statistics (NCES) U.S. Department of Education. Retrieved December 6, 2007.
Materials and Equipment
- Computer with Internet connection
- Printer (and an adult to help you print)
- Centimeter Graph Paper
- Pen
- Scissors
- Tape
- Metric ruler
- Rice or coarse salt (coarse salt is best)
- Metric measuring cup
- NOTE: You may also do this experiment with non-metric cups and spoons, just as long as you stay consistent throughout your project. These instructions are for using metric cups and spoons, so you will need to make adjustments to the instructions accordingly.
Experimental Procedure
- First, you will need to print graph paper that has a 1-centimeter grid so you can measure your images. Here you can print out free sheets of centimeter graph paper. You will need to print three sheets for the shape you test in your experiment.
- Choose a shape (either pyramid, cube, or octahedron) to print from the PBS Kids 2D to 3D Morphing Activity page.
- With the help of an adult, print the shape of your choice in three different sizes by changing the settings on your computer when you print. Use a separate sheet of paper to print each shape. The following steps may vary, depending on what internet browser you use, your computer, and the type of printer you have.
- Select the "print" option in your browser. Ask an adult for help if you cannot find the print button (its location will vary depending on the browser).
- Change the "Scale" setting to one of the following: 100%, 75%, or 50%. Ask an adult for help if you need help finding the "Scale" option (you might have to access another menu like "Print Options" or "Page Layout" first).
- Select "OK" and then print your shape.
- Repeat until you have the shape you chose in three different sizes.
- As you print each sheet, label the shape to keep track of the scale (100%, 75% or, 50%).
- Cut out and assemble the shapes, using scissors and tape. Make sure you tape all of the seams, because you will be filling them with rice or salt later and don't want the ingredient to pour out any of the holes.
- Prepare a data table to keep track of your data. You will be measuring the length of a side, the surface area, and the volume of each 3-D shape. Note that your measurements will be approximate, and you should round to the nearest half centimeter. Here is a sample data table you could use for this experiment:
Shape Scale (%) Length of Edges (cm) Surface Area (cm2) Volume (mL or cm3) 50% 75% 100% - Measure the length of a side of each shape, in centimeters, remembering to round to the nearest half centimeter. Write the values in your data table. Are all of the sides the same length?
- Measure the surface area of each shape by tracing each side of the shape on a sheet of centimeter graph paper. Color in the squares inside the traced area for each side. Count the total number of squares you colored in by adding them together, again rounding to the nearest half-centimeter square. This number represents the surface area of your shape in square centimeters (cm2). If a square is only halfway used on a side, add it to your measurement as one half (1/2) of a square centimeter (1/2 cm2). Write the values in your data table.
- Measure the volume of each shape by filling the shape with rice or salt (coarse salt works best). In order to fill your shapes, loosen the tape for one flap of each shape, lift the flap, and fill to the top with rice or salt. Pour the rice or salt into a metric measuring cup and measure the volume, in milliliters (mL), which is also the volume in cubic centimeters (cm3). Write the values in your data table.
- After you have all the measurements for all of your scaled shapes, it is time to graph your data. Using the information in your data table, make three line graphs of your data. You can also use a resource like the Create a Graph website to make the following bar graphs and print them out for your poster. On each graph, the scale of the shape (50%, 75%, 100%) will be on the left side of the graph (y-axis) and the variable you measured will be on the bottom (x-axis) of the graph. Here is the data you should put on each graph:
- Scale vs. Length (cm)
- Scale vs. Surface Area (cm2)
- Scale vs. Volume (cm3)
- It's time to draw a conclusion! Which geometric property changed the most as you changed the size of your 3-D object: length, surface area, or volume?
- If you want, you can repeat this experiment with the other two Cyberchase shapes.
Ask an Expert
Variations
- How is 3-D geometry used to design packaging? Here is an idea from Cyberchase: "Explore your home to find two-dimensional shapes in different cardboard boxes by taking them apart. Then put them back together! Try finding boxes with irregular shapes, like a cylindrical hat box or an octagonal pizza box!"
- For a more advanced project, you can use geometrical formulas to calculate the properties of the 3-D shapes. One good site where you can look up geometric formulas is the Math.com Geometry page. Here are some examples using the formulas for a cube:
- Instead of counting squares of graph paper to add up the surface area, use the formula for surface area of a cube: (6a2).
- Instead of using rice or salt to measure the volume, use the geometrical formula for the volume of a cube (a3).
- Visit CYBERCHASE Onlineto find more ways to use math to unlock the secrets of science, play math-based interactive games, download free stuff, and more! Extensive resources are also available for parents and teachers.
Careers
If you like this project, you might enjoy exploring these related careers:










